sumproduct() ฟังก์ชันการรวมที่น่าสนใจ

SUMPRODUCT เป็นสูตรที่ใช้สำหรับ การหาผลคูณของคอลัมน์ตั้งแต่ 2 คอลัมน์ขึ้นไป และเอาผลที่ได้จากการคูณนั้น มารวมกัน เช่น

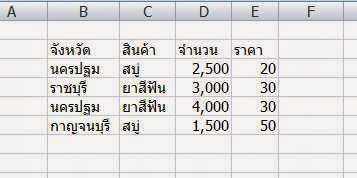
จากภาพ ถ้าเราไม่ใช้ SUMMPRODUCT หาผลรวมของทั้งหมด เราอาจจะหาผลคูณ ของแต่ละรายการ แล้วนำมารวมกัน เป็นผลรวมทั้งหมด เช่น F3 เขียนสูตร D3*E3, F4เขียนสูตร D4*E4 ไปเรื่อย ๆ ...จากนั้น จึงหาผลรวม เช่น ที่ F8 เขียนสูตรว่า Sum(F3:F6) ก็จะได้ ดังนี้

จะเห็นว่า มีการทำงาน 2 ขั้นตอน คือต้องหาผลคูณก่อน แล้วจึงนำมารวมกันอีกครั้ง 

แต่ถ้าใช้สูตร SUMPRODUCT ซึ่งโปรแกรมจะทำงานเช่นเดียวกับข้างต้น คือหาผลคูณแต่ละรายการ และนำผลที่ได้มารวมกัน ข้อแตกต่างคือ ทำเพียงครั้งเดียว และสามารถยืดหยุ่นได้ ซึ่งจะได้แสดงให้ดูต่อไปว่า ยืดหยุ่นได้อย่างไร ผลที่ได้จากการใช้ SUMPRODUCT ในช่อง F8 มีดังนี้

หลักการ

• SUMPRODUCT ต้องการข้อมูลที่เป็น array หรือพูดง่าย ๆ ว่าเป็นข้อมูลชุดที่ติดต่อกัน เช่นในตัวอย่าง เป็นข้อมูลในคอลัมน์
• ถ้ามีมากกว่า 1 คอลัมน์ ข้อมูลนั้น ต้องมีจำนวนเท่ากัน
• เราสามารถเพิ่มความยืดหยุ่น โดยการกำหนดเงื่อนไขในแต่ละคอลัมน์ได้

วิธีการ

1. กรอกข้อมูล ดังภาพ
   
2. ที่ช่อง F8 พิมพ์สูตร และระบุข้อมูล คอลัมน์สินค้า (C3:C6) และราคา (D3:D6) ดังนี้ (ขอให้สังเกตว่า ระหว่างคอลัมน์ เราใช้เครื่องหมายคอมม่า คั่นกลาง ระหว่างช่วงข้อมูลในวงเล็บ)
   
3. หกากากดปุ่ม ENTER จะได้ผลลัพธ์ ตามข้างต้น
4. SUMPRODUCT สามารถยืดหยุ่นได้ โดยเราสามารถสร้างเงื่อนไขให้รวมเฉพาะรายการสบู่เท่านั้น เราเขียนคำสั่งดังนี้
   
5. เงื่อนไขที่เพิ่มเข้ามา คือในช่วง C3:C6 ให้เอาข้อมูลมาเฉพาะที่มีค่าเท่ากับ สบู่ เท่านั้น จะสังเกตเห็นได้ว่า เราคร่อมคำว่า สบู่ ด้วยเครื่องหมายคำพูด และทั้งหมดอยู่ในวงเล็บ และใช้เครื่องหมายคูณ ซึ่งใน Excel ใช้เครื่องหมายดอกจันทร์ (*) เพื่อคูณกับข้อมูลเดิมของเรา
6. เบื้องหลัง คือ โปรแกรมจะไปตรวจสอบก่อนว่า ในช่วง C3:C6 ตามที่เรากำหนดว่ามีตัวใดบ้างที่เท่ากับคำว่า สบู่ ถ้ามี ก็จะให้ค่าเป็นจริง หรือเท่ากับ 1 ถ้าไม่ใช่คำว่า สบู่ ก็จะให้ค่าเป็นเท็จ หรือ มีค่าเป็น 0 ซึ่งเมื่อนำค่าแต่ละแถวมาคูณกัน ถ้าเป็น 0 ผลลัพธ์ก็เป็น 0 ถ้าเป็น 1 ผลลัพธ์ก็จะเท่าเดิม แล้วจึงนำผลที่ได้ทั้งหมดมารวมกัน เป็นผลรวมของสบู่ ดังนี้
   
   หรือ
   
7. ถ้าเราสั่งให้ประเมินสูตรในช่อง F8 (Office 2007-2010 ไปที่แถบ สูตร เลือกดูกลุ่ม ตรวจสอบสูตร และคลิกปุ่ม ประเมินสูตร) ซึ่งในช่อง F8 เราใช้สูตร SUMPRODUCT จะเห็นว่า มีการประเมินผล ก่อนที่จะนำไปคูณ ดังนี้
   
8. จะเห็นว่า การประเมินข้อมูลก่อนที่จะนำไปคูณกัน คือ TRUE FALSE FALSE TRUE หรือ 1 0 0 1 นั่นเอง ซึ่งสอดคล้องกับที่กล่าวมาแล้วข้างต้น

ในกรณีที่มีเงื่อนไขมากกว่า 1 เงื่อนไข

เราใช้หลักการการประเมินเป็น true หรือ false กับเงื่อนไขแต่ละเงื่อนไขเสียก่อน จากนั้นจึงเอาผลมาคูณกัน คือ ถ้า เงื่อนไขทั้ง 2 เป็นจริง ก็จะได้ 1 แต่ถ้าเงื่อนไขใดเงื่อนไขหนึ่งเป็นเท็จ ก็จะได้ 0 ซึ่งส่วนนี้จะเป็นค่าแรกที่ป้อนเข้าสูตร sumproduct จากนั้นจึงกำหนดคอลัมน์ที่ 2 ให้กับสูตร sumproduct ลองดูตัวอย่างจากภาพข้างล่างนี้ 

ถ้าอยากทราบว่า ยอดขายของสมหมาย เดือนมกราคม มียอดเท่าไรจะต้องทำอย่างไร นั่นคือ ต้องมีการกำหนดเงื่อนไข 2 เงื่อนไข

• เงื่อนไขแรก คือ ชื่อ = สมหมาย
• เงื่อนไขที่ 2 คือ เดือน = ม.ค.

ถ้าเงื่อนไขทั้งสองเป็นจริง จึงให้เอาคอลัมน์ที่เป็นยอดขายมารวมกัน (จากในข้อมูล จะเป็นการ ขายสบู่ รวมกับยาสระผม)

สูตรที่ต้องการ จึงมีดังนี้

=SUMPRODUCT((B2:B7="สมหมาย")*(C2:C7="ม.ค."),E2:E7)

ผลการประเมินจากสูตร จะเป็นอย่างนี้

ผลที่ได้คือ

ถ้าคลิกที่ช่อง E10 และให้ประเมินสูตรดู ผลที่ได้ จะเป็น ดังนี้